弧长
用微积分来求曲线的长度。
(请先去阅读关于 导数 和 积分 的内容)
想象我们需要知道一条曲线上两点之间的距离,而这曲线是平滑的(导数是 连续的)。
我们可以把曲线切成小段,然后用 两点之间的距离 的公式来求一个近似值。
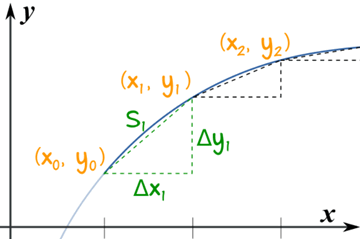
从 x0 到x1:
S1 = √ (x1 − x0)² + (y1 − y0)²
我们用 Δ (delta) 来代表值的差,所以:
S1 = √ (Δx1)² + (Δy1)²
我们需要很多这样的长度:
S2 = √(Δx2)² + (Δy2)²
S3 = √(Δx3)² + (Δy3)²
……
……
Sn = √(Δxn)² + (Δyn)²
我们可以用 总和 的记法把全部的方程写在一个式子里:
可是,我们还是要做很多计算!
我们可以用一个很大的电子表格或者写一个计算机程序来做……不过在这里我们用另一个方法。
一个巧妙的方法:
- 让所有的 Δxi 都是 一样长,那么我们便可以把它们从平方根里拿出来,
- 把总和变成一个积分。
来,开始:
首先,用 Δyi 除以 和 乘以 Δxi:
分解出 (Δxi)²:
把 (Δxi)² 从平方根里拿出来:
当 n 趋向 无穷大时 (趋向无穷多的线段,每段越来越小),总和变成:
这是一个 积分 ,我们用 dx 来代表 Δx 的长度趋向零(dy 也一样):
dy/dx 是函数 f(x) 的 导数,可以写成 f’(x):
弧长公式
我们不但不用计算和相加很多小线段的长度,我们还可以得到一个绝对准确的答案(假设我们可以求公式里的微分和积分)。
注意:这个积分也适用于变量是 y 的函数, x=g(y):
所以步骤是:
- 求 f’(x) 的 导数
- 解 √1 + (f’(x))² dx 的 积分
先看一些简单的例子:
例子:求 f(x) = 2 在 x=2 和 x=3 之间的距离
f(x) 是条水平线,所以导数是 f’(x) = 0
| 开始: | S =
3
∫
2
√1 + (f’(x))² dx
|
|
| 代入 f’(x) = 0: | S =
3
∫
2
√1 + (0)² dx
|
|
| 简化: | S =
3
∫
2
dx
|
|
| 求积分: |
S = (3-2) = 1 |
所以 2 和 3 之间的弧长是 1。答案其实一眼就可以看出来,不过我们至少知道用弧长公式也可以得到正确的答案!
有趣的是: 弧长公式里的 "(1 + ...)" 部分使得答案 至少 是 x 坐标之间的距离,当 f’(x) 等于零时(如上)便是一个例子。

例子:求f(x) = x 在 x=2 和 x=3 之间的长度
导数:f’(x) = 1
| 开始:: | S =
3
∫
2
√1 + (f’(x))² dx
|
|
| 代入 f’(x) = 1:: | S =
3
∫
2
√1 + (1)² dx
|
|
| 简化: | S =
3
∫
2
√2 dx
|
|
| 再简化: | S = √2
3
∫
2
dx
|
|
| 求积分: |
S = √2(3-2) = √2
|
单位正方形对角线的长度是 2 的平方根,对不对?
好,现在来看一些困难但实用的例子:

例子:在峡谷上空每隔6米放一根金属杆。
求形状如以下曲线的索桥的长度:
f(x) = 5 cosh(x/5)
曲线的图如下:
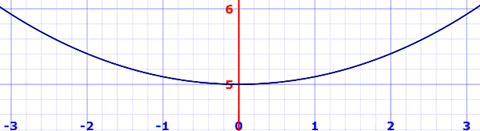
我们先来解一般情况!
悬挂的链的形状是一条叫 悬链线 的曲线:
f(x) = a cosh(x/a)
a 的值越大,线中间下垂越小
"cosh" 是 双曲余弦 函数。
导数是:f’(x) = sinh(x/a)
曲线是对称的,所以只用悬链线从中间到端点"b"的半条来做运算会比较容易:
| 开始: | S =
b
∫
0
√1 + (f’(x))² dx
|
|
| 代入 f’(x) = sinh(x/a): | S =
b
∫
0
√1 + sinh²(x/a) dx
|
|
| 用这个恒等式 1 + sinh²(x/a) = cosh²(x/a): |
S =
b
∫
0
√cosh²(x/a) dx
|
|
| 简化: | S =
b
∫
0
cosh(x/a) dx
|
|
| 求积分: | S = a sinh(b/a) |
因为有对称,我们只算了线的一半,整条线是从 −b 到 +b:
S = 2a sinh(b/a)
在现在的 具体情况中,a=5 并且从 −3 到 +3 是 6米 的距离
S = 2×5 sinh(3/5)
= 6.367米 (精确到最近的毫米)
这个很重要!如果金属杆之间的链的长度是刚好 6米,我们便不能把链拉紧到可以连接两根金属杆,但如果长度是 6.367米就正好了。
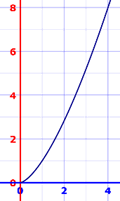
例子:求 y = x(3/2) 在 x = 0 到 x = 4 之间的长度
导数是 y’ = (3/2)x(1/2)
| 开始: | S =
4
∫
0
√1 + (f’(x))² dx
|
|
| 代入 (3/2)x(1/2): | S =
4
∫
0
√1 + ((3/2)x(1/2))² dx
|
|
| 简化: | S =
4
∫
0
√1 + (9/4)x dx
|
我们可以用 换元积分法:
- u = 1 + (9/4)x
- du = (9/4)dx
- (4/9)du = dx
- 上下限:u(0)=1 和 u(4)=10
| 得到: | S =
10
∫
1
(4/9)√u du
|
|
| 求积分: | S = (8/27) u(3/2) 从 1 到 10 | |
| 计算: | S = (8/27) (10(3/2) - 1(3/2)) = 9.073…… |
结论
弧长公式是:
步骤:
- 取 f(x) 的导数
- 写下弧长公式
- 简化并解积分