棱锥

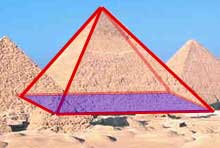
埃及大金字塔
实际上是正四棱锥,因为它们的底面是正方形。
棱锥的部分
棱锥是把底面和顶点连起来而形成的
棱锥种类
有很多不同类型的棱锥,它们的命名是基于底面的形状.
| 棱锥 | 底面 | ||
| 三 棱锥: |
 |
 |
细节 >> |
|---|---|---|---|
| 正四 棱锥: |
 |
 |
细节 >> |
| 五 棱锥: |
 |
 |
细节 >> |
……等等…… |
|||
直棱锥与斜棱锥
这基于顶点的位置。如果顶点是直接在底面的中点之上,它便是个直棱锥,否则便是个斜棱锥。
 |
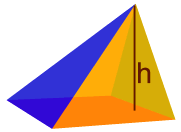 |
| 直棱锥 | 斜棱锥 |
|---|
规则棱锥与不规则棱锥
这是基于底面的形状。如果底面是个规则(正)多边形,它便是个规则(正)棱锥,否则便是个不规则棱锥。
 |
 |
| 规则(正)棱锥 | 不规则棱锥 |
|---|---|
 |
 |
| 底面是规则的 | 底面是不规则的 |
面积与体积
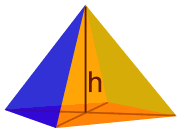
棱锥的体积
-
1/3 × [底面积] × 高
棱锥的表面积
所有侧面相同:
- [底面积] +
1/2 × 周长 × [斜高]
当侧面是不相同时:
- [底面积] + [侧面积]
表面积附注
表面积有两个部分:底面的面积(底面积)和侧面的面积(侧面积)。
底面积:
每个底面图形(三角形、正方形等等)的面积都有不同的公式,你可以在面积页面找到公式,或者用面积计算器来求面积
侧面积:
当侧面相同时:
- 用周长乘以 "斜高",然后除以 2。这是因为侧面一定是三角形,而三角形面积的公式是 "底乘高除 2"
但如果侧面是不相同的(例如是个 "不规则" 棱锥),我们就必须把每一个三角形的面积加起来。