数的演变
让我们一起去体验一个历奇之旅……
……在数字宇宙里的奇妙旅程。
启航!
问:数是什么?
答:用来计数的东西!
数数(正整数)
我们可以用数来计数:1、2、3、4……
从远古开始,人类已经用数来计数。这是个自然不过的行为。
- 你可以有 "3个朋友",
- 田园上可以有 "6头牛"
- 等等。
所以一开始就有:
数数:{1, 2, 3, ...}(数数是英语 "counting number" 的直译,中文通常称为正整数)
在很长一段时间,人类在日常生活里只需要 "数数" 就够用了。
零
零对我们来说是个自然的概念,但对早期的人类则不是这样……如果什么都没有,你怎样计数?
例子:你可以数有多少条狗,但你不能数空间:
 |
 |
|
| 两条狗 | 零条狗?零只猫? |
|---|
空的草地就是空的草地!
位置标志符
大约 3,000年前,人们开始使用零来分辨好像 4 和 40 等的数字,以避免混淆。
人们用一个 "位置标志符",例如空位或特别符号,来显示 "这个位置没有数字"
| 5 2 | 所以 "5 2" 的意思是 "502" (5百,没有十,2个一) |
这就是零的初始概念。一千年后,人们开始把零当作一个数。
我们可以这样想:
"我有 3个橙子,我全都吃了,现在我有零个橙子……!"
整数
把零加到数数中就是一个新数集。
叫 "非负整数":
非负整数:{0, 1, 2, 3, ……}

自然数
非负整數也叫 "自然数",但自然数的定义是存在争议的:
在中国大陆,小学教科书对 "自然数" 定义是这样的:
- 2000年左右以前:不包括 0:{1, 2, 3,……}(就是正整数或数数)
- 2000年左右以后:包括 0:{0, 1, 2, 3,……}
所以如果要绝对清晰,就要声明是否包括零。
负数
数学的历史是充满了询问问题与寻找答案的过程的!
一个好问题是
"如果你可以向一个方向走,你也可以向相反方向走吗?"
我们可以向前数:1、2、3、4……
……那么,反过来数呢? 3、2、1、0…… 接下来是…… |
 |
答案是:负数:

现在可以向前和向后数了
但数怎样可以是 "负" 的?
小于零就是负数。
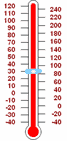 |
一个简单的例子是温度。 我们把摄氏零度(0° C)定义为水结冰的温度……再冷就是负的温度了。 所以−20° C 是零下 20°。 |

负头牛?
理论上可以有负一头牛!
想象这个情形……如果你刚卖了两头公牛,但你只找到一头交给买家……你便是拥有负一头牛……你欠一头牛
所以负数是实际存在的,我们要另一个数集了……
整数
把负整数和非负整数的合并就是一个新数集,称为整数
整数:{……、-3、-2、-1、0、1、2、3、……}
整数包括零、正整数(数数)和负整数,它向正负方向无穷延续。

分数
 |
如果你想和另一个人共享一个橙子,你需要把橙子切成两半。 你发明了一种新的数字! |
你用一个数(1)除以另一个数(2)来得到一半(1/2)
同样,三个人(3)要共享四(4)块饼干……每个人得到(4/3)块。
新数种,叫:
有理数
任何可以写成分数的数就是有理数。
所以,若 "p" 和 "q" 是整数(如上),则 p/q 是个有理数。
例子:若 p 是 3 而 q 是 2,则:
p/q = 3/2 = 1.5 是个有理数
唯一例外是当 q 等于零时,因为除以零是未定义的。
有理数:{p/q:p 和 q 是整数,q 不等于零}
所以一半(½)是个有理数。
2 也是有理数,因为你可以把 2 写为 2/1
所以,有理数包括:
- 所有整数
- 所有分数。
甚至 13.3168980325 也是个有理数。
13.3168980325 = 133,168,980,325 / 10,000,000,000
所有的数都包括在有理数里了,对吗?
可是,还有更多
人就是好奇的……在希腊数学家毕达哥拉斯的时代,有一个很具争议性的问题:
 |
边长为 "1" 的正方形的对角线有多长? |
答案是 2 的平方根,等于 1.4142135623730950……
但它不是一般的数,像 3 或三分之五……
惊艳!有些数不是有理数!它们叫什么?
什么 "不是有理" 的……?无理!
无理数
2 的平方根(√2)是个无理数。它被称为无理数,因为它并不是有理数(不能以两个整数的比来表达)。不是横蛮,只是无理。
我们知道很多无理数。圆周率――Pi (π)是个有名的无理数。
有用
无理数很有用。你需要无理数来
- 计算一些正方形对角线的长度、
- 做很多与圆有关的计算(用π)、
- 还有很多。
所以我们又需要一个
包括无理数的数集……
实数
哈!又一个新名词!
实数包括:
- 有理数、
- 无理数、
实数:{x:x 是有理数或无理数}
实数可以是实数直线上的任何一点:
上面只显示几位小数(它只是个简单的计算器),
但实际上实数可以有很多位小数!
实数直线的任何位置的任何点,应该差不多了吧!
但还有一个非常有用的数种。这数种也是源于一个问题的。
虚想……
问题是:
"负一有平方根吗?"
换句话说,什么数与自己相乘是 −1?
小心想想:一般的数和自己相乘的结果都不会是负数:
- 1×1 = 1,
- (-1)×(−1) = 1(因为负负得正)
什么数与自己相乘是−1?
通常这是不可能的,但是……
"虚幻成真"
因此…….
虚数
 |
……我们虚想负一的平方根存在。 我们甚至给它一个特定符号:拉丁字母 i |
我们可以用它来解答这样的问题:
例子:−9 的平方根是多少?
答案:√(−9) = √(9 × −1) = √(9) × √(−1) = 3 × √(−1) = 3i
答案里还有个 i,但这是个合理并一致的答案。
i 有个有趣的属性。它的平方,(i×i)等于 −1,是个实数。实际上,这是虚数的严格定义:
虚数:一个平方为负实数的数。
并且,i(−1 的平方根)乘以任何实数是个虚数。所以以下的都是虚数:
- 3i
- -6i
- 0.05i
- πi
虚数在很多邻域都很有用,例如电学和电子学。
实数与虚数
当初,虚数被视为不实际的,所以被称为 "虚"数。实数的名称就代表它是实际的。
因此,这些名字都是经过历史过滤的。现实世界里不能只用 "实"数,而虚数也不是"虚无缥缈"的……两种数都同样有用!
其实实数与虚数经常用在一起……
"把实数和虚数结合起来会怎么样?"
复数
把实数与虚数放在一起是一个新数种,叫复数。这是一些例子:
- 3 + 2i
- 27.2 − 11.05i
复数有实部和复部,但每个部分都可以是零:
所以实数也是复数(复部为零):
- 4 是个复数(因为它是 4 + 0i)
同样,虚数也是复数(实部为零):
- 7i 是个复数(因为它是 0 + 7i)
所以复数包括所有实数、所有虚数和所有实数与虚数的组合。
就是这么多!
这就是数学里所有数的种类。
从数数到复数。
也有其他的数,因为数学博大精深,但现在我们就只讲这么多。
总结
这是全部的数种:
| 数的种类 | 简介 |
|---|---|
| 数数(正整数) | {1, 2, 3, ……} |
| 非负整数 | {0, 1, 2, 3, ……} |
| 整数 | {……, -3, -2, -1, 0, 1, 2, 3, ……} |
| 有理数 | p/q:p 和 q 是整数,q 不是零 |
| 无理数 | 非有理数 |
| 实数 | 有理数和无理数 |
| 虚数 | 平方是个负实数 |
| 复数 | 实数与虚数的结合 |
尾注
历史
数学的历史广泛渊远,不同的文化(希腊、罗马、亚拉伯、华夏、印度、欧洲)跟随不同的路径去探索数学,有很多 "谁先发现?" 的问题,但大致上和我这里讲的次序差不多。
问题
敢于发问,像
- "如果反过来数到小于零又怎么样",或
- "正方形的对角线有多长"
这些问题在开始时往往引起争议(甚至嘲笑!),但最终都导致伟大的突破。
今天人们在问什么问题呢?
轮到你了!
每一次学习新东西时,你都应该问这两个问题:
可以反过来吗?
- 正数变成负数
- 平方变成平方根
- 等等
用在其他地方可以吗?
- 如果分数是一个数,我们可以把分数相加、相减等等……吗?
- 可以把复数开方吗?(可以吗?)
- 等等
可能有一天你的问题会导致伟大的突破!